Solution for 9 If y cf(x), where c is a constant and (x) is a differentiable function prove that dy/dx = cf'(x) %3DCalculus Find dy/dx y=1/x y = 1 x y = 1 x Differentiate both sides of the equation d dx (y) = d dx ( 1 x) d d x ( y) = d d x ( 1 x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsM(x,y)dxN(x,y)dy= 0 is defined implicitly by φ(x,y)= c, where φ satisfies (194) and c is an arbitrary constant Proof We rewrite the differential equation in the form M(x,y)N(x,y) dy dx = 0 Since the differential equation is exact, there exists a potential function φ (see (194)) such that ∂φ ∂x ∂φ ∂y dy dx = 0 But this
If X M Y N X Y M N Prove That Dy Dx Y X Sarthaks Econnect Largest Online Education Community
Find dy/dx if x^y y^x=c where c is constant
Find dy/dx if x^y y^x=c where c is constant- Best answer Given, xy = yx Taking logarithm on both sides, we get y log x = x log y Differentiating both sides, wrt x y (1/x) log x (dy/dx) = x (1/y) (dy/dx) log y 1 (y/x) (log x) (dy/dx) = (x/y) (dy/dx) log y (dy/dx) log x (x/y) = log y (y/x) (dy/dx) (y log x x)/ySolution Given differential equation is y d y d x x = c ⇒ y d y = ( c − x) d x On integrating both sides, we get y 2 2 = c x − x 2 2 d ⇒ y 2 x 2 − 2 c x − 2 d = 0 Hence, it represents a family of circles whose centres are on the x axis




Integrate Y With Respect To X Calculus How To
World of mathematics Something went wrong Wait a moment and try againClick here 👆 to get an answer to your question ️ If y = c , a constant then find dy/dx rutvij4873 rutvij4873 Math Secondary School If y = c , a constant then find dy/dx 2 It follows that 1/t = dy/dxlnx> x^y(lnx(dy/dx) y/x) Doing the same, we get that y^x(lny x/y(dy/dx)) Thus the derivative of the entire function is given by x^ylnx(dy/dx) x^y(y/x) y^xln y y^x x/y(dy/dx) = 0 x^ylnx(dy/dx) y^x x/y(dy/dx) = x^y(y/x) y^xlny dy/dx = (x^y(y/x) y^xln y)/(x^ylnx y^x (x/y)) Hopefully this helps!
2 Answers2 Active Oldest Votes 3 d ( y c) = d y d c However, if c is a constant, then d c = 0 so we get d ( y c) = d y Consequently, if one side of the following makes sense, then both sides do and they are equal A general solution of the differential equation \((x y) \frac{dy}{dx} = x y\) will be _____ where c is a constant Q15 The solution of the differential equation \((yx)^2 \dfrac{dy}{dx}=a^2\) is given bySolution For Find (dy)/(dx)\ if (x^2y^2)^2=x y
Dy/dx = x y, which we can think of as slope = x y But isoclines are where slope is constant So let's rewrite the equation again as constant = x y Or, more briefly as x y = C, where C represents any constant A little algebra, (very little), gives us y = x C, A very common integration problem is when we are given an expression for `dy/dx` and we are given a point that the curve passes through and we need the find the original function This is integration because we are told the `dy/dx` and we need to find the original expression Ok, so if I've got `dy/dx` equals 3x 2 2 I recognise that what I need to do is to integrate thisThe derivative of tan(x) tan ( x) with respect to x x is sec2(x) sec 2 ( x) sec2(x) sec 2 ( x) Reform the equation by setting the left side equal to the right side y' = sec2(x) y ′ = sec 2 ( x) Replace y' y ′ with dy dx d y d x dy dx = sec2(x) d y d x = sec 2 ( x)




Math 432 Hw 2 5 Solutions Pdf Free Download




3 A Verify That For Any Constant C The Expression Gauthmath
If xy=c 2, then y=c 2 /x So y/x = c 2 /x 2 You got the same answer, just in a different formKCET 15 If x = ct and y = (c/t) , find (dy/dx) at t=2 (A) (1/4) (B) 4 (1/4) (D) 0 Check Answer and Solution for above question from MathNotice there is no 0th order derivative here Hence, this is actually just a firstorder equation in disguise Substitute v = \frac{dy}{dx} \frac{dv}{dx} = v^2 Separate this and solve v(x) = \frac{1}{c




For Each Of The Following Find Dy Dx Y X 3 E X Chegg Com




Application Of Derivatives
The rate at which y is changing is dy/dx times the rate at which x is changing (that's a rigorous statement) Which is pretty much the same thing as saying that dy/dx is dy divided by dx But you have to keep in mind that this is only a heuristic!Dy/dx = u(dv/dx) v(du/dx) Now, from y = 3xsinx, u will be = 3x, and v = sinx du/dx = 3, and dv/dx = cosx, hence, dy/dx = 3x(cosx) sinx(3) dy/dx = 3sinx 3xcosx Now for the right answer to the above question Option A is incorrect Option B is incorrect C is incorrect D is the correct answer KEYPOINTS You may please note these/this Find a continuous solution satisfying $$ \frac{dy}{dx} y= f(x) $$ Where $$ f(x) = \begin{cases} 1 &\text{ for } 0 < x < 1, \\ 0 & \text{ for } x > 1 \end{cases} $$ w Stack Exchange Network Stack Exchange network consists of 177 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn




1 First Order Ode S 18 03 Exercises
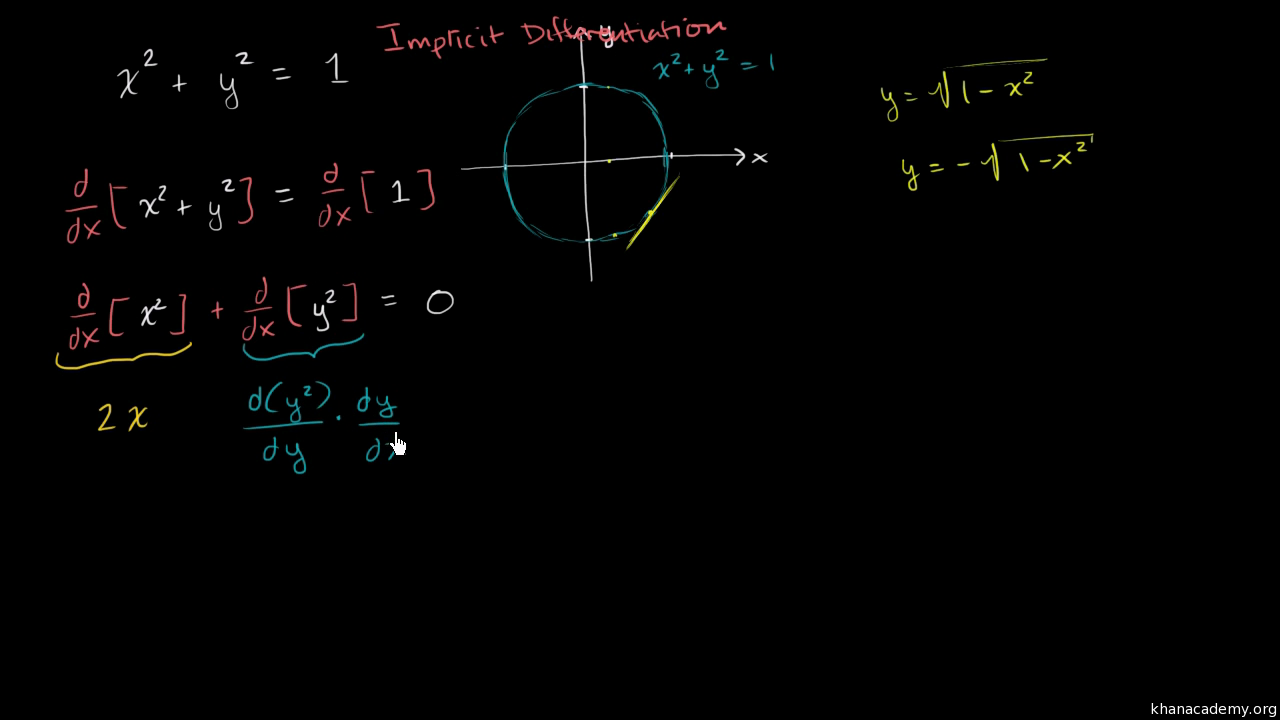



Implicit Differentiation Example Walkthrough Video Khan Academy
Transcribed image text If xy = C, where is a constant, then the corresponding differential equation is α" ₂4 dy dx = 4xy 423 4 y=0 dy 2 dx 4x4y = 0 x ₂4 dy hodiny 4x®y = 0(Write your answer in the form F(x,y) = C, where C stands for an arbitrary constant) {eq}\frac{dy}{dx} = \sqrt4{(\frac{x}{y})} ,or, \frac{dy}{dx} = (\frac{x}{y})^{\frac{1}{4}} {/eq}Answer d //dx=y1/1x Given the equation xy=xy We need to find dy/dx We will use implicit differentiation ==> xy'=xy'




Implicit Differentiation




For Exercises 1 21 Find Dy Dx Assume A B C Are Constants X 2 Y 3 8 Homeworklib
Example 35 Find 𝑑𝑦/𝑑𝑥 , if 𝑥 = 𝑎𝑡2, 𝑦 = 2𝑎𝑡 𝑑𝑦/𝑑𝑥 = 𝑑𝑦/𝑑𝑥 × 𝑑𝑡/𝑑𝑡 𝑑𝑦/𝑑𝑥 = 𝑑𝑦/𝑑𝑡 × 𝑑𝑡/𝑑𝑥 𝑑𝑦/𝑑𝑥 = (𝑑𝑦/𝑑𝑡)/(𝑑𝑥/𝑑𝑡) Calculating 𝒅𝒚/𝒅𝒕 𝑦 = 2𝑎𝑡" "𝑑𝑦/𝑑𝑡 " " = 𝑑(2𝑎𝑡)/𝑑𝑡 𝑑𝑦/𝑑𝑡 = 2𝑎 𝑑(𝑡)/𝑑𝑡 𝑑𝑦/𝑑𝑡 = 𝟐𝒂Calculating 𝒅𝒙/𝒅𝒕 Prachi Agarwal answered this x = ct dx/dt = d/dt ( ct ) = c * d/dt ( t) t * d/dt (c) applying product rule = c (1) t (0) difft of t is 1 and difft of constant c is 0 = c ie, dx/dt = c now, y = cWe have the following theorem Theorem 1



Deriving The Derivative Of Inverse Tangent Or Y Arctan X Youtube



Derivative Of X X Youtube
Uploaded By Army_Dillo Pages 6 This preview shows page 2 4 out of 6Now suppose we find the derivative of y with respect to a, but TREAT x as the constant Then dy da = x Here we just "reversed" the roles played by a and x in our equation Example 11 For f(x,y,z) use the implicit function theorem to find dy/dx and dy/dz 1 f(x,y,z)=x 2y3 z xyz Example 24 Find 𝑑𝑦/𝑑𝑥 if 𝑥 − 𝑦 = 𝜋 (x − y) = 𝜋 Differentiating both sides wrt x (𝑑(𝑥 − 𝑦))/𝑑𝑥= 𝑑𝜋/𝑑𝑥 𝑑𝑥/𝑑𝑥− 𝑑𝑦/𝑑𝑥 = 0 1 − 𝑑𝑦/𝑑𝑥 = 0 𝒅𝒚/𝒅𝒙 = 1 (As 𝜋 is constant)



If X Y Y X What Is Dy Dx Quora




11 A Find The Derivative Of The Function X Is A Chegg Com
(Use C as an arbitrary constant) Variable Separable Equation Any differential equation that can be written in the form, {eq}h\left( x \right)dx = k\left( y \right)dy {/eq}, is a differentialCourse Title COST ACCOU 1;RHS x log(2) => log(2) log(2) is a constant so x dissapears So we get (1/y)(dy/dx) = log(2) 4) We want to find dy/dx, which is on the LHS To get this dy/dx on its own we can multiply both sides by y So we get dy/dx = y log(2) 5) To finish this question we need to sub in for y and then we have an answer for dy/dx




Solve The Following Differential Equation Given That Y 1 When



Ocw Mit Edu Courses Urban Studies And Planning 11 2 Planning Economics Fall 10 Related Resources Mit11 2f10 Calcnotes Pdf
X c Cancelling the logarithm from both sides of the above equation, we get y = x c This is the required solution of the given differential equation ⇐ Solve Differential Equation dy/dx=xe^y ⇒ Separable Variables of Differential Equations ⇒Solution of ` (x y)^2 (dy)/ (dx)=a^2` ('a', being a constant) is solution of ` (x y)^2 (dy)/ (dx)=a^2` ('a', being a constant) is Watch later Share Copy link Info Shopping And now i am clueless how to find C Becouse I cannot find arctan pi/4 and there is a problem with pi^2/161 I assume that C=0 becouse graphic of arctan x and 1/(x^21) are very close in point 079 (pi/4), but i cannot prove it




Misc 15 If X A 2 Y B 2 C2 Prove 1 Dy Dx 2 3 2



Www Open Edu Openlearn Ocw Mod Resource View Php Id
Solution For Find (dy)/(dx)if xy =pi LIVE Classes starting 15 th June 21 30 Students 90 Days 24x7 Video Doubt Support ₹ ₹8000 KNOW MOREClick here👆to get an answer to your question ️ If y = x^x , then find dydxFind dy/dx if x^2y^2=2xy A x/(xy) B (yx)/(yx) C 1 D x/y E None of these 93,270 results, page 4 All answers in this problem should be numerical Find the value of the constant c c= Find P(Y Calculus A rectangle is bounded by the xaxis and the semicircle y = sqrt(36x^2) What length and width should the rectangle have so that



If X M Y N X Y M N Prove That Dy Dx Y X Sarthaks Econnect Largest Online Education Community
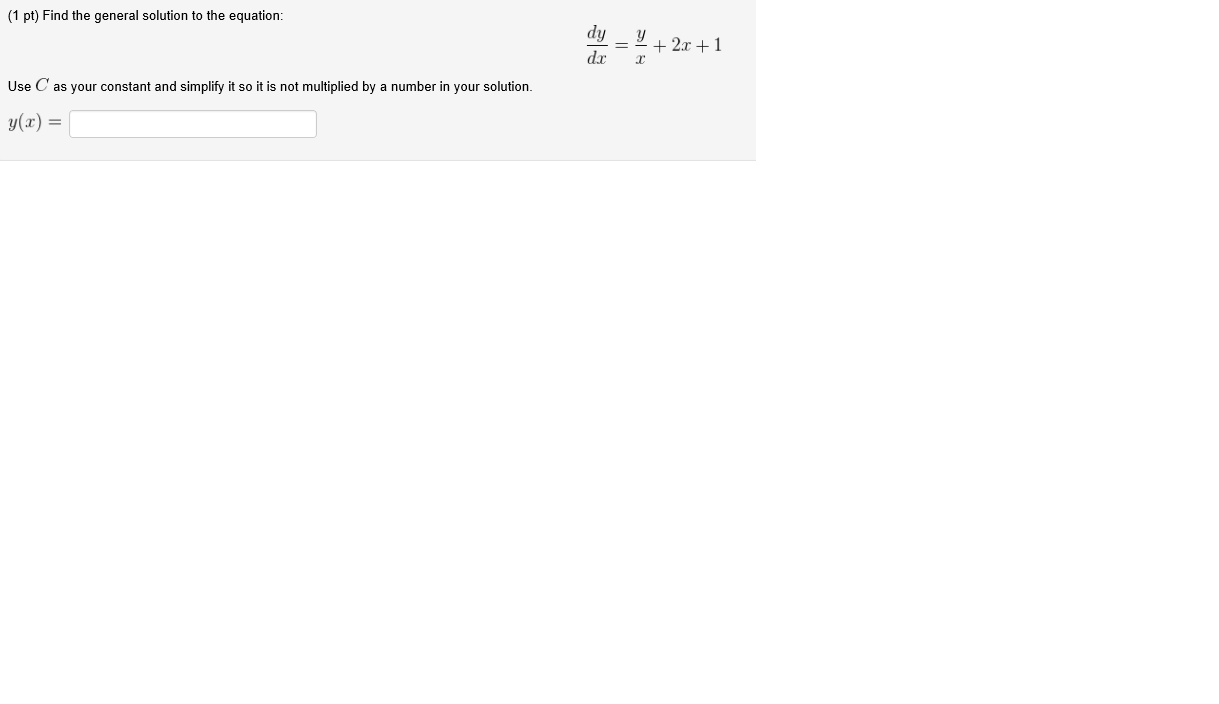



Find The General Solution To The Equation Dy Dx Chegg Com
If x y y x = a b, find dy/dx cbse;Find dy dx y c cos x x 2 sin x c is constant 2 pts A c cos x x cos x sin x C c Find dy dx y c cos x x 2 sin x c is constant 2 pts a School Ateneo de Davao University;(x 3y)dx (x 2y)dy = 0 Existence of a solution The general solution of the equation dy/dx = g(x, y), if it exists, has the form f(x, y, C) = 0, where C is an arbitrary constant Under what circumstances does a general solution exist?




How To Do Implicit Differentiation 7 Steps With Pictures



Q Tbn And9gcqfrqxr507ozco1lhgiqwot Cdchophjbocrnsjhblpnw2oyhom Usqp Cau
If x=at2 and y=at, then find dy/dx?If x^2y^2 =25 and dy,dt =6, find dx,dt when y=4Solution for dx/dy px = q, where p and q are functions of y or constants A differential equation is called linear if there are no multiplications among dependent variables and their derivatives In other words, all coefficients are functions of independent variables It can be written in two forms The second is discussed in detail here




Integrate Y With Respect To X Calculus How To




Ma 104 Differential Equations
Answer x^(y1) y y^x logy/1 x^y logx x y^(x1) Solution y = x^y y^x Let u = x^y and v = y^x Then, y = u v and dy/dx = du/dx dv/dx(1) We will now find du/dx and dv/dx separately and substitute iThis might appear to have no solutions given y(0) = 1, but as it turns out the constant y= 1 is itself a solution 5 dy dx = e yx;y(0) = 2 e y dy= ex dx e y = c ex e y = c ex y= ln( c ex) y= ln(1 1=e ex) Note that this solution will not be de ned for all values of x, since ln(x) is only de ned for positiveIn Introduction to Derivatives (please read it first!) we looked at how to do a derivative using differences and limits Here we look at doing the same thing but using the "dy/dx" notation (also called Leibniz's notation) instead of limits We start by calling the function "y" y = f(x) 1 Add Δx When x increases by Δx, then y increases by Δy



Implicit Differentiation




Product Distribution Wikipedia
We can neglect C ′ C' C ′ since another integral constant C C C is hidden in the integral ∫ f (x) d x \int f(x)~dx ∫ f (x) d x Therefore, we can conclude that if d y d x = f (x), \frac{dy}{dx}=f(x), d x d y = f (x), then y = ∫ f (x) d x C y=\int f(x)~dxC y = ∫ f (x) d x C Find y y y in terms of x x x where d y d x = xClick here👆to get an answer to your question ️ If y^x = x^y , then find dy/dxFind an answer to your question if x^y y^x = c find dy by dxplease give answer with simple steps




Notation For Differentiation Wikipedia




Implicit Differentiation Example Walkthrough Video Khan Academy
Find y 0 so that the integral curve for dy/dx=xy y(4)=y 0 is a straight line You must justify your answer, which will require you to apply algebraic reasoning to the problem I know the answer is 3 I also know this differential equation looks simple, but IShare It On Facebook Twitter Email 1 Answer 1 vote answered by paayal (147k points) selected by Vikash Kumar Best answer Put x y = u and y x = v ∴ (i) becomesHere we will look at solving a special class of Differential Equations called First Order Linear Differential Equations First Order They are "First Order" when there is only dy dx, not d 2 y dx 2 or d 3 y dx 3 etc Linear A first order differential equation is linear when it can be made to look like this dy dx P(x)y = Q(x) Where P(x) and Q(x) are functions of x To solve it there is a




Worked Example Euler S Method Differential Equations Video Khan Academy




Ex 5 5 15 Find Dy Dx Of Xy E X Y Class 12 Ex 5 5




Example 24 Find Dy Dx If X Y Pi Chapter 5 Ncert Examples




Eyzqfgnna2tanm




Implicit Differentiation




If Y Cos Xy Then Find Dy By Dx Brainly In




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12




Ex 5 5 12 Find Dy Dx Xy Yx 1 Class 12 Cbse Ncert




Math For Intermediate Economics




Engineering Mathematics Notes



1




Math 432 Hw 2 5 Solutions Pdf Free Download



5 Derivative Of The Logarithmic Function




Find An Equation Of The Tangent Line To The Graph Of Chegg Com



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf




Partial Derivative Examples Math Insight




Find The Complete Solution Of Left Frac Dy Dx Right 2 Frac Y X Frac Dy Dx Frac A X 0 Where A Is A Positive Constant Holooly Com




7 8 Differential Equations Variables Separable




Ncert Books For Class 12 Maths Chapter 9 Differential Equation



If X Y Y X What Is Dy Dx Quora




15 6 Calculating Centers Of Mass And Moments Of Inertia Mathematics Libretexts



If X Y Y X What Is Dy Dx Quora
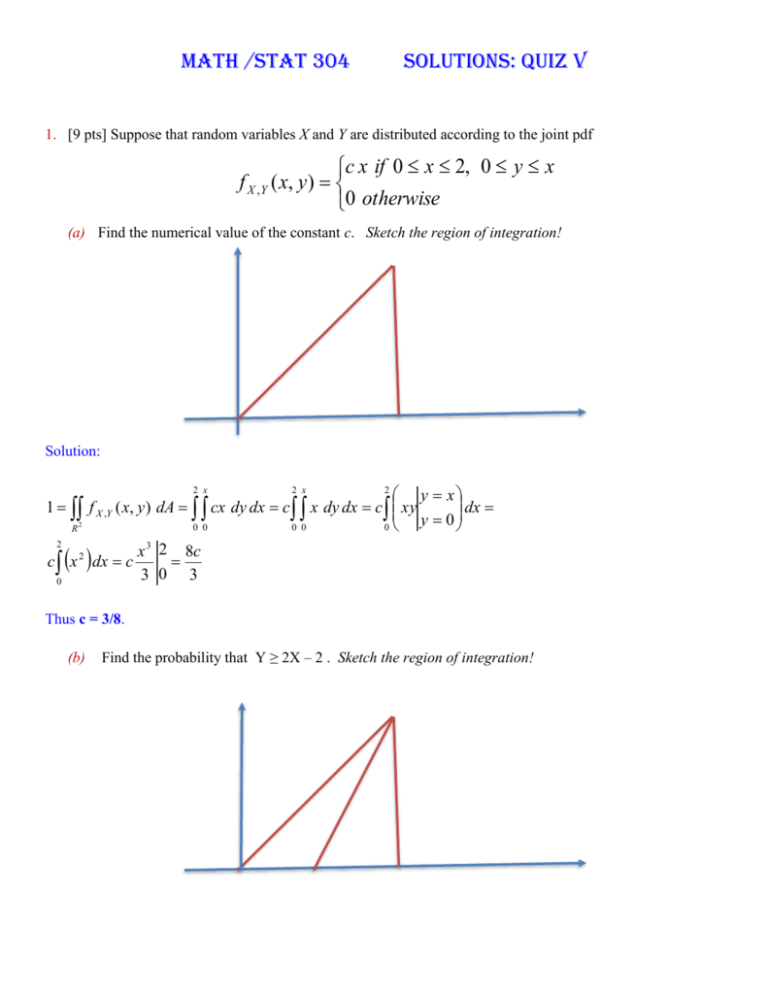



Math Stat 304 Solutions Quiz V




Homogeneous Differential Equations



Www Osti Gov Servlets Purl




Engineering Mathematics Notes



Rules Of Calculus Functions Of One Variable



1



Math Vanderbilt Edu Peters10 Teaching Fall08 Hwsolutions3 Pdf




Notes 9 09 Independence Studocu



Find Dy Dx If Y X X Y A B Where A B Are Constants Sarthaks Econnect Largest Online Education Community



2




Engineering Mathematics Notes



The Derivative




Worked Example Euler S Method Differential Equations Video Khan Academy



16 1 2 Variables Separable Equations



Www Amherst Edu System Files Multivariable 25review 25session 253 Pdf




Differentiating Related Functions Intro Video Khan Academy




Example 33 Find Dy Dx If Y X X Y X X A B Teachoo




Engineering Mathematics Notes



Increasing And Decreasing Functions




If X Y Y X Then Find Dydx



Http Www Thphys Physics Ox Ac Uk People Jamesbinney Mt Pdf




Tutorial 7 Ordinary Differential Equation Equations



Search Q Chain Rule Tbm Isch




If X2 Y2 2 Xy Find Dy Dx Mention Each And Every Step Mathematics Topperlearning Com Gwvwfskk




Partial Derivative Examples Math Insight




Engineering Mathematics Notes




If Y X In Cx Where C Is An Arbitrary Constant Is The Gener



How To Differentiate W R T X Xy C 2 Quora



How To Solve This Equation Dy Dx Sin X Y Quora




How Do You Find Dy Dx When X A Cost Tsint And Y A Sint Tcost Socratic




None Is Defective Is 10 If 2x Y 4x 7 7y 13 Then The




If Y X X Y X Y X Y Find Dy Dx




Answered C Given That F Axyi X Y J Is Bartleby



2



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q4 Pdf



2




If Y X In Cx Where C Is An Arbitrary Constant Is The Gener
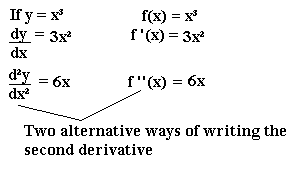



The Second Derivative Mathematics A Level Revision




Derivative Rules




Verify That Y X Cx C 2 Where C Is A Constant Chegg Com



Integrating Factor Method



Find Dy Dx When X And Y Are Connected By The Following Relations Sarthaks Econnect Largest Online Education Community



Double Integrals



Http Pages Stat Wisc Edu Ifischer Calculus Pdf
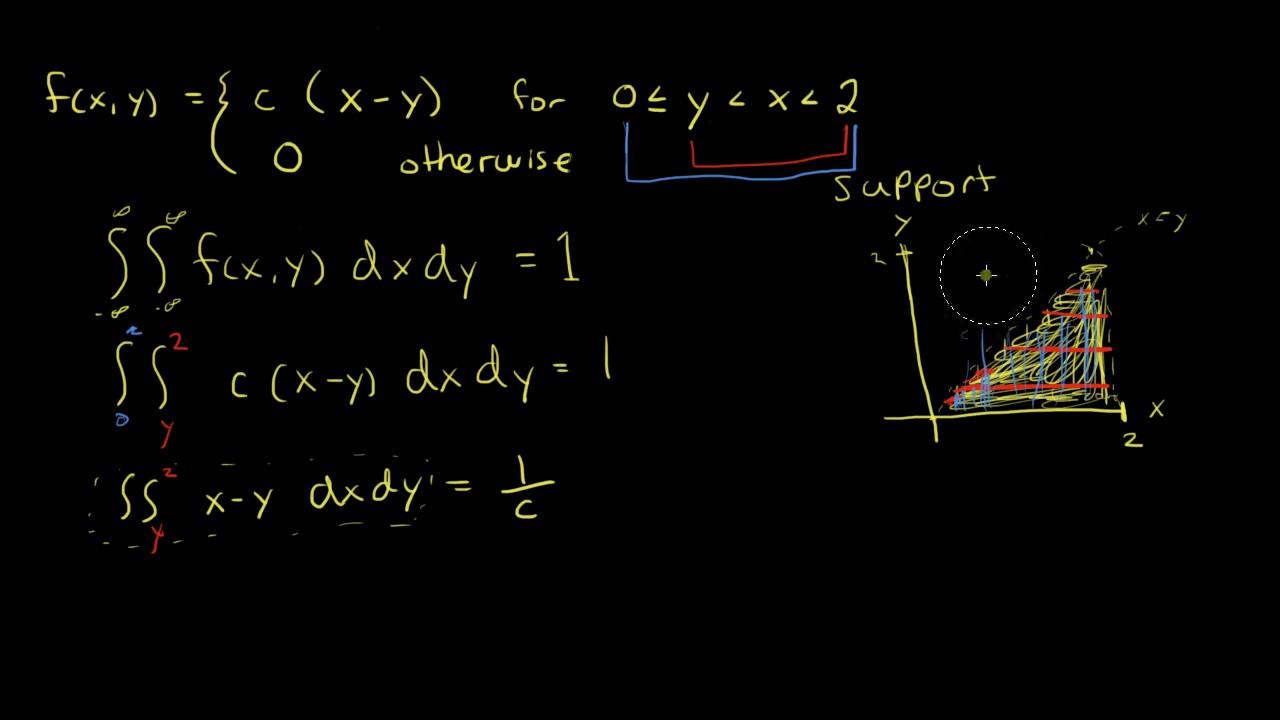



Joint Pdf Find The Constant Youtube




How To Do Implicit Differentiation 7 Steps With Pictures




Mutual Information Wikipedia




If X 1 Y Y 1 X 0 Then Prove That 1 X 2 Dydx 1 0




Xy C 2 Then Dy Dx Please Answer In Full Brainly In



2




Ex 5 3 6 Find Dy Dx In X3 X2y Xy2 Y3 81 Cbse



2




How To Do Implicit Differentiation 7 Steps With Pictures
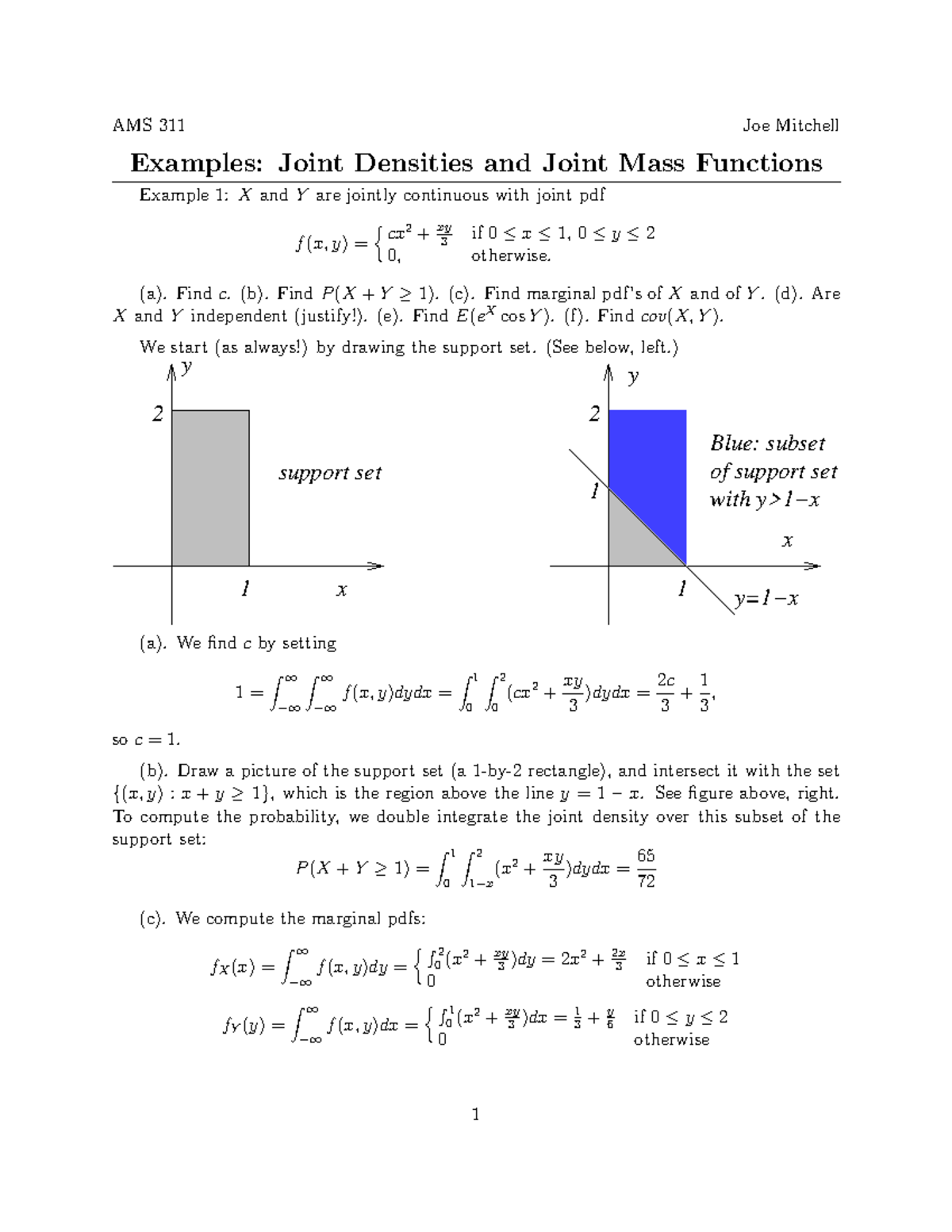



Examples Joint Pdfs Sol Studocu



What Is The Derivative Of 1 X Quora




X Ct Y C T Find Dy Dx Brainly In


